All posts in this series:
- One Potato: A description of the problem
- Two potato: The basic equations
- Three potato: An algebraic formula for the last person left
- Four: A neat calculation method using binary numbers
- Five potato: F# functions to check the various formulae
- Six potato: Using a calculation graph to see the pattern
- Seven potato: Generalizing to other intervals
- More: An efficient algorithm for arbitrary intervals
- Online research: In which I discover that it is called the Josephus problem
Introduction
In the first four posts in the series I derived Mathematical formulae for calculating the last person left in a circle if every second person is asked to leave (continuing until only one person remains).In this post I am going to write F# scripts to check these formulae.
Why F#?
- Functional programming languages often express Mathematical concepts very elegantly
- I felt like learning a functional language (though I had originally planned to learn Haskell)
- I opened the F# interactive console on a whim and the solutions were flowing before I had time to change my mind!
I'm very happy with how natural it felt to use F#. And it does build on my knowledge of .Net. So I don't regret my somewhat accidental choice of F# instead of Haskell.
Brute force computation
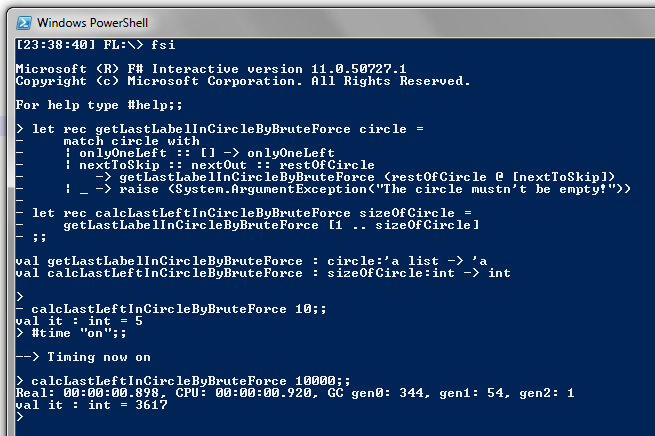
The following F# functions use a brute force approach to calculate the number of the last person left in the circle:let rec getLastLabelInCircleByBruteForce circle =
match circle with
| onlyOneLeft :: [] -> onlyOneLeft
| nextToSkip :: nextOut :: restOfCircle
-> getLastLabelInCircleByBruteForce (restOfCircle @ [nextToSkip])
| _ -> raise (System.ArgumentException("The circle mustn't be empty!"))
let calcLastLeftInCircleByBruteForce sizeOfCircle =
getLastLabelInCircleByBruteForce [1..sizeOfCircle]
Here's a short explanation of the F# syntax...
- "let rec <functionName> <parameter> =" defines a recursive function taking a single parameter.
- F# is strongly typed. It uses Hindley-Milner type inference to deduce parameter types.
- "match circle with" does pattern matching on circle.
- Each pipe ("|") is the start of a pattern. Whatever comes after "->" is the result if the pattern is the first to match.
You will also need to know a few things about lists in F#. I recommend reading this wikibooks article or this article by Microsoft's Chris Smith.
Note the following...
- F# lists are linked lists, not the .Net List class.
- "head::tail" is a list comprising an element called head pointing to a sub-list called tail.
- "[]" is an empty list.
- So "onlyOneLeft :: []" matches a list with a single item (the answer).
- "nextToSkip :: nextOut :: restOfCircle" matches the first two items in the list. restOfCircle is the remaining people in the circle (which could be the empty list).
- "_" is a placeholder which will match anything.
- "list1 @ list2" concatenates two lists.
- "[1..N]" creates a list with the numbers 1, 2, 3, ... N.
So the algorithm repeatedly moves the first person to the end of the list and skips the second person. It does this recursively until a single person is left. If you like, we are rotating the circle towards us, instead of moving around the circle (which would involve unnecessary complexity, such as keeping track of our current position and clocking over correctly when we reached the end of the list).
Let's run the fsi application and calculate the results for circles with 10 and 10,000 people (with timing switched on):
This appears to be quite slow. It took around 0.9 seconds to run the calculation for a circle with 10,000 people.
This is partly because "(restOfCircle @ [nextToSkip])" is an O(n) operation, where n is the size of restOfCircle.
Recursive computation
In the second post in the series I derived the basic equations needed to solve the problem:$$ \begin{align*} f(1) &= 1 \tag{1} \\ f(2n) &= 2.f(n) - 1 \tag{2} \\ f(2n+1) &= 2.f(n) + 1 \tag{3} \end{align*} $$
My second F# script uses these equations to calculate the solution:
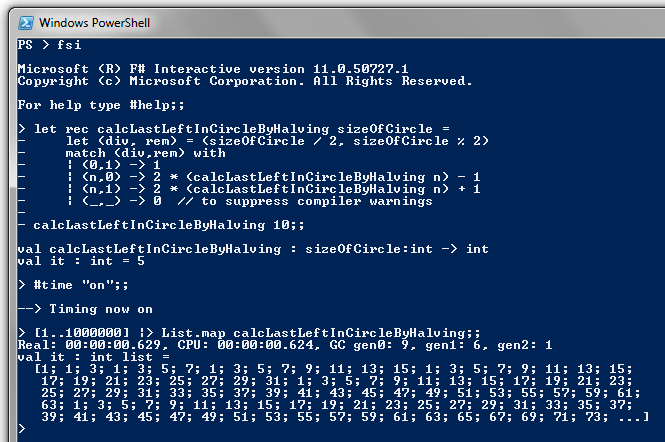
let rec calcLastLeftInCircleByHalving sizeOfCircle =
let (div, rem) = (sizeOfCircle / 2, sizeOfCircle % 2)
match (div,rem) with
| (0,1) -> 1
| (n,0) -> 2 * (calcLastLeftInCircleByHalving n) - 1
| (n,1) -> 2 * (calcLastLeftInCircleByHalving n) + 1
| (_,_) -> 0 // to suppress compiler warnings
Notice how closely the first 3 patterns correspond to the 3 formulae.
The code also runs much faster than the brute force approach. So much faster that it calculated all the numbers up to a million in 0.629 seconds!
Computation via the algebraic formula
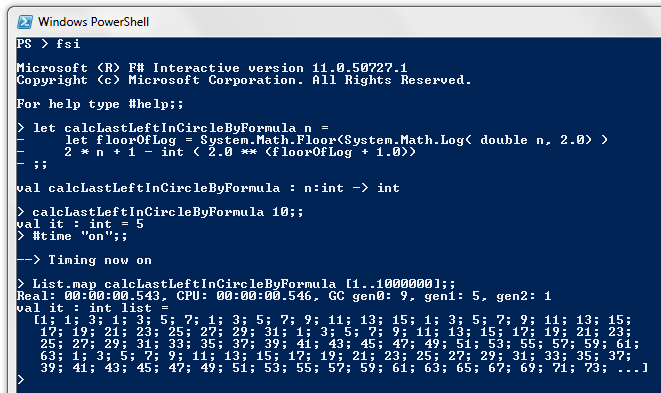
In my third post of the series I derived an algebraic formula for the last person left in the circle: $$ f(n) = 2n + 1 - 2^{{\lfloor log_2 n \rfloor} + 1} \tag{9} $$ In F# this becomes:let calcLastLeftInCircleByFormula n =
let floorOfLog = System.Math.Floor(System.Math.Log( double n, 2.0) )
2 * n + 1 - int ( 2.0 ** (floorOfLog + 1.0))
Note that System.Math is the static class in the .Net framework for Mathematical calculations. Its Log() method has an overload which takes the base of the logarithm as its second parameter.
Running this for all the numbers up to a million takes 0.543 seconds - slightly quicker than the previous method...
Two things make me uncomfortable with this approach:
- It feels inefficient to be doing floating point calculations to solve an integer problem.
- I'm concerned that rounding errors could cause a calculation error
Computation via binary arithmetic
In the fourth post in the series I presented a very elegant rule for calculating the answer using binary representations.This method can be re-stated (for computational convenience) as follows:
- take the binary representation of the number
- drop the leading digit
- shift left
- add 1
Let's convert that to F#:
First we need to find the leading digit, so we can drop it. This is equivalent to finding the highest power of 2 that is less than (or equal to) the number. In other words it's the term $2^{\lfloor log_2 n \rfloor}$ in the algebraic formula.
This is the same as finding the left-most bit in the binary representation of the number and setting all remaining bits to zero.
We can do this easily by repeatedly shifting the number to the right (the final bit drops out) and simultaneously shifting the number 1 to the left each time (this multiplies by 2, giving the next higher power of 2). Repeat until the original number is 1, and the other number will be the power of 2 we are looking for.
In F# the ">>>" operator does a bitwise right shift, and "<<<" does a left shift. So the following pair of F# functions calculate $2^{\lfloor log_2 n \rfloor}$:
let rec calcFirstBinaryDigit powerOf2 shiftedNumber =
match shiftedNumber with
| 0 -> raise (System.ArgumentException("No power of 2 is less than zero"))
| 1 -> powerOf2
| _ -> calcFirstBinaryDigit (powerOf2 <<< 1) (shiftedNumber >>> 1)
let calcHighestPowerOfTwoNotGreaterThan = calcFirstBinaryDigit 1
With this building block in place, we can easily express the binary calculation method as follows:
let calcLastLeftInCircleByBinaryFormula n =
((n - calcHighestPowerOfTwoNotGreaterThan n) <<< 1) + 1
The binary formula took 0.465 seconds, which is marginally faster than the floating point formula:
Comparing the results of the various methods
Now let's return to the original purpose of writing these various F# scripts, which was to check the Mathematics.First I'm going to create a data structure to hold all the answers from the various methods for a single size of circle...
type circleCalculation = {
SizeOfCircle: int;
LastLeftInCircleByBruteForce: int;
LastLeftInCircleByHalving: int;
LastLeftInCircleByFormula: int;
LastLeftInCircleByBinaryFormula: int
}
Then I'm going to create a function to perform the calculation of a single record. I want this function to have a parameter allowing me to switch off the brute force method if I want to, since I know it is much slower than the other methods:
let getCircleCalculation includeBruteForce sizeOfCircle =
// Brute force is so slow to calculate. Provide the option to omit it...
let lastLeftInCircleByBruteForce =
match includeBruteForce with
| true -> calcLastLeftInCircleByBruteForce sizeOfCircle
| false -> 0
let lastLeftInCircleByHalving = calcLastLeftInCircleByHalving sizeOfCircle
let lastLeftInCircleByFormula = calcLastLeftInCircleByFormula sizeOfCircle
let lastLeftInCircleByBinaryFormula = calcLastLeftInCircleByBinaryFormula sizeOfCircle
let circleCalc = {
SizeOfCircle = sizeOfCircle;
LastLeftInCircleByBruteForce = lastLeftInCircleByBruteForce;
LastLeftInCircleByHalving = lastLeftInCircleByHalving;
LastLeftInCircleByFormula = lastLeftInCircleByFormula;
LastLeftInCircleByBinaryFormula = lastLeftInCircleByBinaryFormula
}
circleCalc
Something that really amazed me is that I didn't need to specify the circleCalculation type in the function. F# is able to infer the data type from the usage pattern. Very neat!
With this in place, I can use the following script to check that the methods all match up:
// With brute force:
[1..1000] |> List.map (getCircleCalculation true) |> List.filter (
fun cc -> cc.LastLeftInCircleByBinaryFormula <> cc.LastLeftInCircleByBruteForce
|| cc.LastLeftInCircleByBinaryFormula <> cc.LastLeftInCircleByHalving
|| cc.LastLeftInCircleByBinaryFormula <> cc.LastLeftInCircleByFormula
)
// Without brute force:
[1..1000000] |> List.map (getCircleCalculation false) |> List.filter (
fun cc -> cc.LastLeftInCircleByBinaryFormula <> cc.LastLeftInCircleByHalving
|| cc.LastLeftInCircleByBinaryFormula <> cc.LastLeftInCircleByFormula
)
Running this shows that all the methods produce the same result. Mission accomplished...
Next time
In the next blog post in the series, I will show a different way of solving the problem. Instead of using the basic equations to recursively calculate a large number from the formula for smaller numbers, I'm going to work in the opposite direction.What will emerge from this is a pattern of answers for successive values of the circle size. You might like to have a look at some of the earlier screen captures to see if you can work out what the pattern is.