Andrew Tweddle's Blog: Seven potato (generalizing to other intervals)

All posts in this series:

One Potato: A description of the problem
Two potato: The basic equations
Three potato: An algebraic formula for the last person left
Four: A neat calculation method using binary numbers
Five potato: F# functions to check the various formulae
Six potato: Using a calculation graph to see the pattern
Seven potato: Generalizing to other intervals
More: An efficient algorithm for arbitrary intervals
Online research: In which I discover that it is called the Josephus problem

Introduction

In the previous posts in the series I derived Mathematical formulae for calculating the last person left in a circle if every second person is asked to leave (continuing until only one person remains).

But what if we want to remove every third person from the list, or every eighth person (as in the "One Potato, Two potato" children's game)?

In this post and the next I will attempt to generalize the results to arbitrary intervals.

The challenge

Let $f_k(n)$ be the label of the last person left in a circle of $n$ people when every $k^{\text{th}}$ person is asked to leave.

Clearly $f_k(1) = 1$.

When the interval is two, the basic equations allowed us to express $f_{2}(2n+b)$ in terms of $f_{2}(n)$. My gut feel is that this same method won't be useful for an interval of $k$, because it will only allow us to express $f_k(kn+d)$ in terms of $f_k((k-1)n)$, not in terms of $f_k(n)$.

Instead I'm going to find a way to express $f_k(n)$ in terms of $f_k(n-1)$.

Interestingly, the inspiration for doing this comes from the generalization of the F# brute force calculation method presented in the fifth blog post in the series. So not only have the functional algorithms proved useful for checking the Mathematics. They have also led to new Mathematical insights!

Brute force computation

So to recap, let's write an F# script which generalizes the brute force calculation method to arbitrary intervals:

let rec getLastLabelInCircleWithIntervalByBruteForce numberToSkip interval circle =
    match (numberToSkip, circle) with
    | (_, current :: []) -> current
    | (0, current :: restOfCircle)
        -> getLastLabelInCircleWithIntervalByBruteForce
            (interval-1) interval restOfCircle
    | (negativeToSkip, _) when negativeToSkip < 0
        -> raise (System.ArgumentException("The number to skip can't be negative!"))
    | (positiveToSkip, current :: restOfCircle)
        -> getLastLabelInCircleWithIntervalByBruteForce
             (positiveToSkip-1) interval (restOfCircle @ [current])
    | (_,_) -> raise (System.ArgumentException("The circle mustn't be empty!"))

let rec calcLastLeftInCircleWithIntervalByBruteForce interval sizeOfCircle = 
    getLastLabelInCircleWithIntervalByBruteForce
        (interval-1) interval [1 .. sizeOfCircle]

The method recursively skips a person and moves them to the end of the list until it reaches the next person to remove from the circle. It removes that person and starts over with the next person to skip being at the front of the list.

It runs in a similar time to the previous brute force algorithm.

A recursive formula

Let's consider what happens when we have $n$ people in a circle, and we remove the next person. Let $m$ be the label of the next person removed from the circle. As with the F# algorithm, after removing person $m$, we will shift the entire circle around so that person $m+1$ is the first person in the list (or person 1 if $m = n$).

So after removing person $m$ and shifting everyone around, we are left with $n-1$ people in the circle: $$ \begin{array}{| l | c | c | c | c | c | c | c |} \hline \text{Index: }& 1 & 2 & \ldots & n-m & n-m+1 & \ldots & n-1\\ \text{Label: }& m+1 & m+2 & \ldots & n & 1 & \ldots & m-1\\ \hline \end{array} $$
We will be using the "mod" (modulo) operator to handle the clocking over from position n to position 1. To do this we need to modify the labels to be zero-based:

$$ \begin{array}{| l | c | c | c | c | c | c | c |} \hline \text{Index: }& 1 & 2 & \ldots & n-m & n-m+1 & \ldots & n-1\\ \text{Label - 1: } & m & m+1 & \ldots & n-1 & 0 & \ldots & m-2\\ \hline \end{array} $$
Note that $n-1 = (n-1) \bmod n$ and $0 = n \bmod n$. This suggests a way of expressing all the labels in a uniform manner:

$$ \begin{array}{| l | c | c | c | c | c | c | c |} \hline \text{Index: } & 1 & 2 & \ldots & n-m & n-m+1 & \ldots &n-1\\ \text{Label - 1: } & m\bmod n & (m+1)\bmod n & \ldots & (n-1)\bmod n & n\bmod n & \ldots & (n+m-2)\bmod n\\ \hline \end{array} $$
Now is a good time to make the labels one-based again. I'll also rearrange the terms slightly to make the mapping from indexes to labels more obvious:

$$ \begin{array}{| l | c | c | c | c |} \hline \text{Index: }& 1 & 2 & \ldots & n-1\\ \text{Label:} & [1+(m-1)]\bmod n + 1 & [2+(m-1)]\bmod n + 1 & \ldots & [(n-1) + (m-1)]\bmod n + 1\\ \hline \end{array} $$
This gives us a way of mapping from indexes to labels. The $i^{\text{th}}$ label in the list is $[i+(m-1)] \bmod n + 1$.

There are now $n-1$ people in the circle. So the index of the last person left will be $f_k(n-1)$. Hence the label of the last person left will be $[f_k(n-1)+m-1]\bmod n + 1$. Hence:

$$ f_k(n) = [f_k(n-1)+m-1]\bmod n + 1 \tag{1} $$
$m$ is the label of the first person removed from the circle of n people. How do we determine $m$?

If $k \le n$ then $m = k$. But what if $k > n$? In this case the circle will be circumnavigated one or more times before the $k^{\text{th}}$ person is eliminated.

We can use the modulo operator to determine the value of m, remembering that we must first zero-base the label, then apply the modulo operator, then add back 1 to the label at the end. So:

$$ \begin{align*} m = & (k-1) \bmod n + 1 & \text{for }k > n \\ m = & k & \text{for } k \le n \end{align*} $$

But these two equations can be collapsed into one, because when $k \le n$ then $k-1 < n$, so $k = (k-1) \bmod n + 1$. So this gives: $$ m = (k-1) \bmod n + 1 \tag{2} $$
Substituting into equation 1, we get the following:

$$ \begin{align*} f_k(n) &= [f_k(n-1) + ((k - 1) \bmod n + 1) - 1] \bmod n + 1 \\ &= [f_k(n-1) + (k - 1) \bmod n ] \bmod n + 1 \tag{3} \\ \text{So: }\\ f_k(n) &= [f_k(n-1) + k - 1 ] \bmod n + 1 \tag{4} \end{align*} $$
As promised, we have a recursive formula for $f_k(n)$ in terms of $f_k(n-1)$.

F# code for the recursive formula

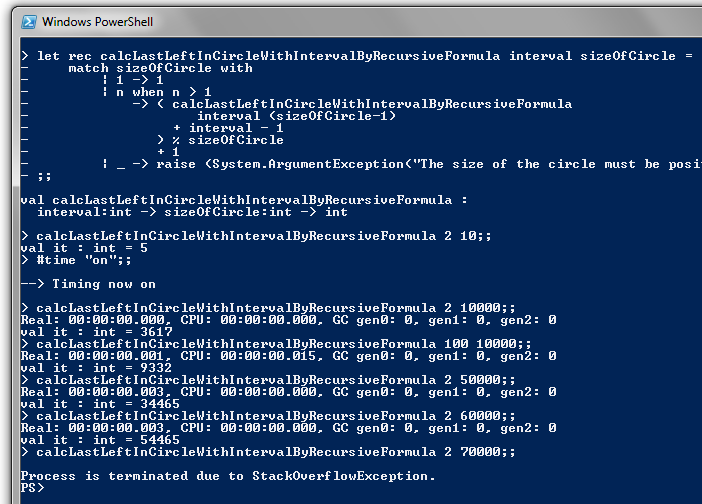
The following F# function implements the recursive formula:

let rec calcLastLeftInCircleWithIntervalByRecursiveFormula interval sizeOfCircle =
    match sizeOfCircle with
        | 1 -> 1
        | n when n > 1 
            -> ( calcLastLeftInCircleWithIntervalByRecursiveFormula
                    interval (sizeOfCircle-1)
                 + interval - 1
               ) % sizeOfCircle
               + 1
        | _ -> raise (System.ArgumentException("The size of the circle must be positive!"))

This function runs much faster than the brute force approach. However it has a significant flaw. On my machine, a stack overflow occurs at some value of $n$ between 60 000 and 70 000. This is not really surprising, since the size of the stack is O(n) and the recursive call is not tail recursive.

By contrast, the recursive formula from the fifth post in the series was O(log n) in the stack size, since it expressed $f_{2}(2n+b)$ in terms of $f_{2}(n)$.

Next time

My next blog post will be a continuation of this topic.

I will be deriving a more efficient algorithm which has O(log n) recursive calls rather than O(n). This will not only solve the stack overflow problem. It will also make the algorithm incredibly fast.

Andrew Tweddle's Blog

Thursday, June 06, 2013

Seven potato (generalizing to other intervals)