All posts in this series:
- One Potato: A description of the problem
- Two potato: The basic equations
- Three potato: An algebraic formula for the last person left
- Four: A neat calculation method using binary numbers
- Five potato: F# functions to check the various formulae
- Six potato: Using a calculation graph to see the pattern
- Seven potato: Generalizing to other intervals
- More: An efficient algorithm for arbitrary intervals
- Online research: In which I discover that it is called the Josephus problem
Introduction
In my previous post I generated a recursive equation for calculating the last person left in a circle if every $k^{\text{th}}$ person is removed from the circle.I also wrote an F# program which highlighted a weakness of this algorithm. For circles with more than 60 000 people, the F# algorithm would experience a stack overflow.
In this post I am going to develop a more efficient algorithm to address this flaw.
Warning: Lots of algebra ahead!
The initial formatting of the Mathematical equations can be slow. If so, please be patient.
The recursive equation for arbitrary intervals
To recap, here is the main equation from the previous blog post: $$ f_k(n) = [f_k(n-1) + k - 1 ] \bmod n + 1 \tag{4} $$[This is very much a continuation of the previous post, so I have gone with the same equation numbering].
Arranging the function outputs in rows
Recall the calculation graph from post 6 in the series:Notice how $f(n)$ "clocks over" for the first value in each row.
Let's arrange the values of $f_k(n)$ into rows in a similar way. To do this I am going to consider the values of $n$ at which $f_k(n)$ clocks over. Every time this happens, a new row will be started.
Let $r$ be the index of a row in the graph.
Let $n_r$ be the first value of $n$ in row $r$.
Now consider the previous value of $n$: $n_r - 1$. Since the modulo operator clocks over for $n_r$, we can take the argument to this operator in equation 4, and we must have:
$$ \begin{align*} f_k(n_r - 1) + k - 1 &\ge n_r \\ \therefore f_k(n_r - 1) &\ge n_r - (k - 1)\\ \end{align*} $$
However, we also know - by the definition of $f_k(n)$ - that:
$$ f_k(n_r - 1) <= n_r - 1 $$
So it must be that:
$$ \begin{align*} f_k(n_r - 1) &= n_r - j & \text{for some } j \in \mathbb{N} \text{ such that } 1 \le j \le k-1 \tag{5} \end{align*} $$
From our definition of $n_r$ we know that $f_k(n)$ doesn't clock over for any $n \in \left\{n_{r-1}+1, n_{r-1} + 2, ..., n_r - 1\right\}$.
And because it doesn't clock over, we can remove the mod operator in equation 4, which simplifies to: $$ \begin{align*} f_k(n) &= [f_k(n-1) + k - 1 ] \bmod n + 1 & \text{from equation 4}\\ &= [f_k(n-1) + k - 1 ] + 1 \\ &= f_k(n-1) + k & \forall n \in \left\{n_{r-1}+1, n_{r-1} + 2, ..., n_r - 1\right\} \\ \\ \therefore f_k(n_{r-1} + i) &= f_k(n_{r-1}) + ik &\forall i \in \left\{0, 1, \ldots, n_r - n_{r-1}-1 \right\} \tag{6} \\ \\ \text{In particular:} \\ f_k(n_r - 1) &= f_k(n_{r-1}) + k.(n_r - n_{r-1} - 1) \tag{7} \\ \end{align*} $$
Equations 5 and 7 give us two different formulae for $f_k(n_r-1)$, so we can combine them: $$ \begin{align*} n_r - j &= f_k(n_{r-1}) + k.(n_r - n_{r-1} - 1)\\ \Leftrightarrow (k-1).n_r &= k.n_{r-1} + k - j - f_k(n_{r-1}) \tag{8} \end{align*} $$
First we are going to use equation 8 to determine the value of j.
We can re-arrange equation 8 as follows: $$ \begin{align*} j - 1 & = k.n_{r - 1} + k - 1 - f_k(n_{r-1}) - (k-1).n_r \\ & = [(k-1)+1].n_{r - 1} + (k-1) - f_k(n_{r-1}) - (k-1).n_r \\ & = n_{r-1} - f_k(n_{r-1}) + (k-1).[n_{r - 1} + 1 - n_r] \tag{9} \end{align*} $$
Why $j-1$ on the left side of the equation?
Recall from equation 5 that $1 \leq j \leq k-1 $. So $0 \leq j - 1 \leq k-2 < k-1$.
And hence $j - 1 = (j - 1) \bmod (k - 1)$. This allows us to simplify the right hand side of equation 9 by taking the "$\bmod (k-1)$" of both sides.
So: $$ \begin{align*} j - 1 & = [j - 1] \bmod (k - 1) \\ & = [n_{r-1} - f_k(n_{r-1}) + (k-1).[n_{r - 1} + 1 - n_r]] \bmod (k - 1) & \text{from equation 9} \\ & = [n_{r-1} - f_k(n_{r-1})] \bmod (k - 1) & \text{since multiples of }k - 1\text{ can be removed} \\ \\ \Rightarrow j & = [n_{r-1} - f_k(n_{r-1})] \bmod (k - 1) + 1 \tag{10} \end{align*} $$
Now that we have a formula for j, we can determine both $n_r$ (using equation 8) and $f_k(n_r)$ (using equations 4 and 5).
Let's determine $n_r$ first. Substituting equation 10 into equation 8 gives:
$$ \begin{align*} (k-1).n_r &= k.n_{r-1} + k - j - f_k(n_{r-1}) &\text{from equation 8} \\ &= k.n_{r-1} + k - ([n_{r-1} - f_k(n_{r-1})] \bmod (k - 1) + 1) - f_k(n_{r-1}) &\text{from equation 10} \\ &= [(k-1) + 1].n_{r-1} + (k-1) - [n_{r-1} - f_k(n_{r-1})] \bmod (k - 1) - f_k(n_{r-1}) \\ &= (k-1).n_{r-1} + n_{r-1} + (k-1) - [n_{r-1} - f_k(n_{r-1})] \bmod (k - 1) - f_k(n_{r-1}) \\ &= (k-1)[n_{r-1} + 1] + n_{r-1} - f_k(n_{r-1}) - [n_{r-1} - f_k(n_{r-1})] \bmod (k - 1) \\ \Rightarrow n_r &= n_{r-1} + 1 + \frac{n_{r-1} - f_k(n_{r-1}) - [n_{r-1} - f_k(n_{r-1})] \bmod (k - 1) }{k-1} \\ \end{align*} $$ This rather complicated quotient can be simplified quite significantly by observing that: $$ \frac{m - m \bmod d}{d} = \lfloor \frac{m}{d} \rfloor $$
This follows by expressing $m$ as: $$ \begin{align*} m &= qd+r & \text{where }0 \leq r < d &\text{i.e. }r = m \bmod d \\ \Rightarrow q & = \frac{m - r}{d} \\ & = \frac{m - m \bmod d}{d} \\ \text{But: } q = \lfloor \frac{m}{d} \rfloor &\text{and the result follows} \end{align*} $$
So substituting $n_{r-1} - f_k(n_{r-1})$ for $m$ and $k-1$ for $d$ we obtain the following simplification:
$$ n_r = n_{r-1} + 1 + \lfloor \frac{n_{r-1} - f_k(n_{r-1}) }{ k - 1 } \rfloor \tag{11} $$
Now let's determine the value of $f_k(n_r)$:
$$ \begin{align*} f_k(n_r) &= [f_k(n_r - 1) + k - 1 ] \bmod n_r + 1 & \text{from equation 4} \\ &= [(n_r - j) + k - 1 ] \bmod n_r + 1 & \text{from equation 5} \\ &= [k - 1 - j] \bmod n_r + 1 \\ &= [k - 1 - ([n_{r-1} - f_k(n_{r-1})] \bmod (k - 1) + 1)] \bmod n_r + 1 & \text{from equation 10} \\ &= [k - 2 - [n_{r-1} - f_k(n_{r-1})] \bmod (k - 1)] \bmod n_r + 1 \end{align*} $$
This is already sufficient. However we can simplify things further. When $n_r \ge k-1$, the $ \text{mod }n_r $ can be dropped. This gives the following set of formulae:
$$ \begin{align*} f_k(n_{1}) & = f(1) = 1 \tag{12} \\ f_k(n_r) & = k - 1 - [n_{r-1} - f_k(n_{r-1})] \bmod (k - 1) & \text{ where } n_r \geq k - 1 \tag{13} \\ f_k(n_r) & = [k - 2 - [n_{r-1} - f_k(n_{r-1})] \bmod (k - 1)] \bmod n_r + 1 & \forall n_r \text{ where } r > 1 \tag{14} \\ \end{align*} $$
So equations 11 through to 14 provide formulae for:
- $n_r$ in terms of $n_{r-1}$ and $f_k(n_{r-1})$
- $f_k(n_r)$ in terms of $n_r$, $n_{r-1}$ and $f_k(n_{r-1})$
- $n_1$ and $f_k(n_1)$
With these pieces in place we are ready to create a more efficient algorithm for calculating $f_k(n)$ for arbitrary n.
The row-based algorithm
Given a value $n$ for which we wish to calculate $f_k(n)$, we can't work backwards down to $f_k(1)$ as we have done in the past. The problem is that we don't know which row $r$ it falls within, or what $n_r$ and $f(n_r)$ are.Instead we are going to have to work our way forwards to find the row that $n$ belongs in. We will start at $n_{1} = 1, f_k(1) = 1$. From this we will derive $n_{2}$ and $f(n_{2})$. We will continue generating this sequence of values for $n_r$ and $n_{r+1}$ until we find a value of $r$ for which $n_r \le n < n_{r+1}$. When we do, we can use equation 6 to determine $f_k(n)$: $$ f_k(n) = f_k(n_r) + k.(n-n_r) \tag{15} $$
While working our way through the rows we will keep track of the values for the next row: $n_{r+1}$ and $f_k(n_{r+1})$. This will allow us to easily calculate $n_{r+2}$ and $f_k(n_{r + 2})$.
Below is an F# function to calculate these values for the next row:
let getNextRowStartSizeAndLabel thisRowStartSize thisRowStartLabel interval =
let floor
= int( System.Math.Floor( double(thisRowStartSize - thisRowStartLabel)
/ double(interval - 1) )
)
let nextRowStartSize = thisRowStartSize + 1 + floor
let nextRowStartLabel =
if nextRowStartSize < interval - 1 then
( interval - 2
- (thisRowStartSize - thisRowStartLabel) % (interval - 1)
) % nextRowStartSize + 1
else
interval - 1 - (thisRowStartSize - thisRowStartLabel) % (interval - 1)
(nextRowStartSize, nextRowStartLabel)
The variables map to the formula as follows:
- thisRowStartSize $\mapsto n_r$
- thisRowStartLabel $\mapsto f_k(n_r)$
- interval $\mapsto k$
- nextRowStartSize $\mapsto n_{r+1}$
- nextRowStartLabel $\mapsto f_k(n_{r+1})$
The following F# functions use the function above to calculate $f_k(n)$:
let rec getLabelOfLastLeftInCircleWithIntervalByRow
thisRowStartSize thisRowStartLabel
nextRowStartSize nextRowStartLabel
interval sizeOfCircle =
if (sizeOfCircle >= thisRowStartSize) && (sizeOfCircle < nextRowStartSize) then
thisRowStartLabel + interval * (sizeOfCircle - thisRowStartSize)
else
let (newNextRowStartSize, newNextRowStartLabel)
= getNextRowStartSizeAndLabel nextRowStartSize nextRowStartLabel interval
getLabelOfLastLeftInCircleWithIntervalByRow
nextRowStartSize nextRowStartLabel
newNextRowStartSize newNextRowStartLabel
interval sizeOfCircle
let calcLastLeftInCircleWithIntervalByRow interval sizeOfCircle =
if sizeOfCircle < 1 then
raise (System.ArgumentException("The size of the circle must be positive!"))
if interval < 2 then
raise (System.ArgumentException("The interval must be 2 or more!"))
let (nextRowStartSize, nextRowStartLabel) = getNextRowStartSizeAndLabel 1 1 interval
getLabelOfLastLeftInCircleWithIntervalByRow
1 1 nextRowStartSize nextRowStartLabel interval sizeOfCircle
The efficiency of the row-based algorithm
Look back at equation 11:$$ n_r = n_{r-1} + 1 + \lfloor \frac{n_{r-1} - f_k(n_{r-1})}{k-1} \rfloor $$
Consider what happens as $n_{r-1}$ starts becoming large compared to $k$. $f_k(n_{r-1}) \le k$ (since a "clock-over" occurs at $n_{r-1}$), so this term will become very small. So as $n_{r-1}$ becomes large:
$$ n_r \approx (1 + \frac{1}{k-1}).n_{r-1} $$
So the $\left\{n_r\right\}$ series is approximately a geometric progression. Since its values are going to grow exponentially, the algorithm will rapidly find the row containing n, even for very large values of n. The size of the stack is going to scale as O(log n), so we are far less likely to reach a value of n which will cause stack overflows.
If we run the latest F# algorithm it is indeed blindingly fast:
It was able to handle some very large 32 bit numbers almost instantaneously.
I would expect it to fail when the next higher $n_r$ value is larger than the maximum 32 bit integer. It might be possible to work around this by inserting a "try catch" block to detect and recover from this situation, since we can still calculate the answer using the previous value of $n_r$.
I thought that another failure condition could be with very large values of $k$, since the exponential growth rate would be very small when $k$ is large. So I tested the algorithm with $k$ and $n$ both equal to a billion (one thousand million). The calculation took slightly under 32 seconds on my i5 laptop.
Displaying the rows in the row-based algorithm
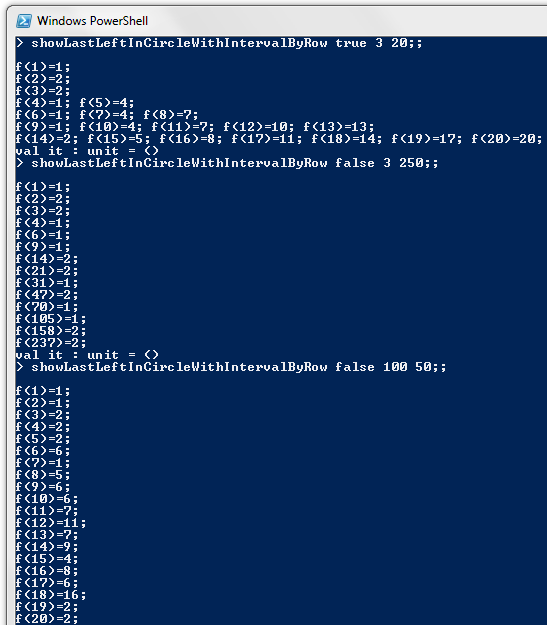
Ideally we would like a closed form solution for arbitrary k. I tried looking for patterns in the rows for various values of k, but I couldn't see a consistent pattern.For anyone who would like to try, or just if you're curious to see the row structure in action, here is an F# script to allow you to see all $(n, f_k(n))$ pairs arranged in rows. It depends on the function getNextRowStartSizeAndLabel defined earlier, so make sure that function has been defined in your F# interactive session:
let rec showLabelsOfLastLeftInCircleWithIntervalByRow
showFullRow thisRowStartSize thisRowStartLabel
nextRowStartSize nextRowStartLabel interval
sizeOfCircle maxSizeOfCircle =
if (sizeOfCircle <= maxSizeOfCircle) then
let result = thisRowStartLabel + interval * (sizeOfCircle - thisRowStartSize)
if sizeOfCircle = thisRowStartSize then
System.Console.WriteLine()
System.Console.Write( "f({0})={1}; ", sizeOfCircle, result)
elif showFullRow then
System.Console.Write( "f({0})={1}; ", sizeOfCircle, result)
if sizeOfCircle < nextRowStartSize - 1 then
showLabelsOfLastLeftInCircleWithIntervalByRow
showFullRow thisRowStartSize thisRowStartLabel
nextRowStartSize nextRowStartLabel
interval (sizeOfCircle+1) maxSizeOfCircle
else
let (newNextRowStartSize, newNextRowStartLabel) =
getNextRowStartSizeAndLabel nextRowStartSize nextRowStartLabel interval
showLabelsOfLastLeftInCircleWithIntervalByRow
showFullRow nextRowStartSize nextRowStartLabel
newNextRowStartSize newNextRowStartLabel
interval (sizeOfCircle+1) maxSizeOfCircle
let showLastLeftInCircleWithIntervalByRow showFullRow interval maxSizeOfCircle =
if maxSizeOfCircle < 1 then
raise
( System.ArgumentException(
"The maximum size of the circle must be 1 or more!")
)
if interval < 2 then
raise
( System.ArgumentException(
"The interval must be 2 or more!")
)
let (nextRowStartSize, nextRowStartLabel) =
getNextRowStartSizeAndLabel 1 1 interval
showLabelsOfLastLeftInCircleWithIntervalByRow
showFullRow 1 1
nextRowStartSize nextRowStartLabel interval
1 maxSizeOfCircle
System.Console.WriteLine()
When the showFullRow parameter to the function is false, then only the first pair in each row will be shown. I find this is a lot more useful than seeing the intermediate values as well, which soon leads to each console line overflowing.
Validating the various algorithms against one other
The following F# script can be used to check that the 3 algorithms produce the same answers:
type circleCalculationWithInterval = {
SizeOfCircle: int;
Interval: int;
LastLeftInCircleByBruteForce: int;
LastLeftInCircleByRecursiveFormula: int;
LastLeftInCircleByRow: int
}
let getCircleCalculationWithInterval includeBruteForce interval sizeOfCircle =
// Brute force is slow to calculate. Provide the option to omit it...
let lastLeftInCircleByBruteForce =
match includeBruteForce with
| true -> calcLastLeftInCircleWithIntervalByBruteForce interval sizeOfCircle
| false -> 0
let lastLeftInCircleByRecursiveFormula =
calcLastLeftInCircleWithIntervalByRecursiveFormula interval sizeOfCircle
let lastLeftInCircleByRow =
calcLastLeftInCircleWithIntervalByRow interval sizeOfCircle
let circleCalc = {
SizeOfCircle = sizeOfCircle;
Interval = interval;
LastLeftInCircleByBruteForce = lastLeftInCircleByBruteForce;
LastLeftInCircleByRecursiveFormula = lastLeftInCircleByRecursiveFormula;
LastLeftInCircleByRow = lastLeftInCircleByRow
}
circleCalc
You can then check the results using snippets similar to the following:
// With brute force:
[1..1000] |> List.map (getCircleCalculationWithInterval true 2) |> List.filter (
fun cc -> cc.LastLeftInCircleByRow <> cc.LastLeftInCircleByBruteForce
|| cc.LastLeftInCircleByRow <> cc.LastLeftInCircleByRecursiveFormula
);;
[1..100] |> List.map (getCircleCalculationWithInterval true 100) |> List.filter (
fun cc -> cc.LastLeftInCircleByRow <> cc.LastLeftInCircleByBruteForce
|| cc.LastLeftInCircleByRow <> cc.LastLeftInCircleByRecursiveFormula
);;
// Without brute force:
[1..10000] |> List.map (getCircleCalculationWithInterval false 2) |> List.filter (
fun cc -> cc.LastLeftInCircleByRow <> cc.LastLeftInCircleByRecursiveFormula
);;
[1..10000] |> List.map (getCircleCalculationWithInterval false 100) |> List.filter (
fun cc -> cc.LastLeftInCircleByRow <> cc.LastLeftInCircleByRecursiveFormula
);;
A new proof for the formula when removing every second person
We can use the general formulae to provide a new derivation of the closed form solution when every second person is removed from the circle.The proof ends up being remarkably simple, because $k - 1 = 1$. Terms such as $(...) \bmod (k-1)$ simply fall away, since any integer mod 1 is zero. Also some terms involve a division by $k-1$, and these also simplify very nicely.
But these simplifications only work for $k = 2$. This reduces my confidence of finding a closed form solution for the general case.
Anyway, here's the proof:
$$ \begin{align*} f_2(n_r) & = k - 1 - [n_{r-1} - f_k(n_{r-1})] \bmod (k - 1) & \text{ from equation 13, since } n_r \geq k - 1 = 1 \\ & = 2 - 1 - [n_{r-1} - f_2(n_{r-1})] \bmod 1 & \text{(but any number mod 1 is 0)} \\ & = 1 & \text{ for }n_r > 1 \\ \\ \text{but: } f_2(n_{1}) & = f(1) = 1 & \text{from equation 12} \\ \\ \therefore f_2(n_r) & = 1 & \forall n_r \tag{16} \\ \\ n_r & = n_{r-1} + 1 + \lfloor \frac{n_{r-1} - f_k(n_{r-1}) }{ k - 1 } \rfloor & \text{ from equation 11} \\ & = n_{r-1} + 1 + \lfloor n_{r-1} - f_k(n_{r-1}) \rfloor & \\ & = n_{r-1} + 1 + n_{r-1} - f_k(n_{r-1}) & \text{(since floor has an integer argument)} \\ & = n_{r-1} + 1 + n_{r-1} - 1 & \text{since }f_k(n_{r-1}) = 1 \text{ by equation 16 } \\ & = 2.n_{r-1} & \text{a geometric progression} \tag{17} \\ \\ \therefore n_r & = 2^{r-1} & \text{by equations 16 and 17} \tag{18} \\ \\ f_2(n) & = f_2(n_r) + 2.(n-n_r) & \text{from equation 15, where: } n_r \le n < n_{r+1} \\ & = 1 + 2(n - 2^{r-1}) & \text{ where: } 2^{r-1} \le n \le 2^r \text{(by equation 18)}\\ & = 1 + 2n - 2.2^{r-1} & \text{where: } 2^{r-1} \le 2^{log_2 n} < 2^r \\ & = 1 + 2n - 2.2^{\lfloor log_2 n \rfloor} & \text{since: } 2^{r-1} = 2^{\lfloor log_2 n \rfloor} < 2^{r}\\ & = 2n + 1 + 2^{{\lfloor log_2 n \rfloor} + 1} \tag{19} \\ \end{align*} $$
And this is the same equation derived in blog post three in the series, albeit through a completely different method.
Conclusion
In this blog post and the previous post I derived formulae which are applicable to intervals other than 2.I was able to use these formulae to find a new proof of the closed form solution for the original interval of 2 (i.e. removing every second person from the circle).
I wasn't able to derive a closed form solution for arbitrary intervals. However I was able to devise an efficient algorithm for calculating the answer.
Next time
I feel that I have progressed as far as I can with the problem on my own. I don't know whether a closed form solution exists. But even if it does, I doubt I'm going to find it.So now it's time to search the internet to see if this is a problem which other people have solved. In my next blog post, I hope to report back on what I found.
I'm also hoping to share some of the scripts and tools I used to generate the artefacts in this series of blog posts.
But most of all, I'm looking forward to wrapping up this series, so that I can move on to other topics that capture my interest!


No comments:
Post a Comment