Overview
In a previous blog post, I showed that the number of squares of various sizes in an nxn grid is $\sum_{{i}={1}}^{n}i^2 $. As n gets large, it's going to take a long time to sum up all those squares. So a closed form solution would be much better.
In this blog post I'm going to demonstrate a very mechanical way of finding that formula. It doesn't require any flashes of genius, and it generalizes to many similar problems. If you were the manager of a team of Mathematicians selling commercial Mathematics projects, this is probably how you'd want them to solve the problem. It's boring, predictable, general and doesn't require (nor provide) any special insight. And you can even solve the algebra programmatically, which will reduce the risk of a calculation error. Kaching!
What? You don't work for a company that sells Mathematics for money? How surprising. Well, stay tuned to this blog series. Because in future blog posts I'm going to present a variety of more inspired solutions. These will give much better insight into why the formula comes out the way it does. But first let's derive the formula...
All posts in this series
- Counting squares in a grid
- Guessing a closed form solution for the sum of squares
- A combinatorial solution for counting squares in a grid
The mechanical approach
Step 1: guess the pattern of the formula
The degree of a polynomial is the highest power that the variable is raised to. If the summation is over a polynomial of degree $d$, then make an educated "guess" that the closed form expression is a polynomial of degree $d+1$. This seems plausible, because it holds for the following well known formulae: $$ \begin{align*} \sum_{{i} = {1}}^{n}1 &= n \\ \sum_{{i} = {1}}^{n}i &= \frac{n(n+1)}{2} &= \frac{1}{2} n^2 + \frac{1}{2} n \\ \end{align*} $$
Firstly, let $f(n) = \sum_{{i}={1}}^{n}i^2 $ be the actual sum of squares function.
Note that $f(0) = 0$ since there are no terms to add when $n = 0$ (there are zero squares in a zero by zero grid).
Now let $g(n)$ be our guess for the closed form equivalent of function f: $$ \begin{align*} g(n) &= \sum_{{j}=0}^{d+1}a_j.n^j \\ &= a_{0} + a_{1} n + a_{2} n^{2} + a_{3} n^{3} & \text{since d = 2} & \tag{1} \end{align*} $$
Next we need to calculate values for the $a_j$ values. We will start with $a_0$.
Step 2: Ensure that $g(0) = f(0) = 0$
$ g(0) = a_3 . 0^3 + a_2 . 0^2 + a_1 . 0 + a_0 = a_0 $
Hence set: $a_0 = 0 \tag{2}$
Step 3: Choose a method for determining the other coefficients
At this point it's tempting to set $g(1) = f(1)$, $g(2) = f(2)$ and $g(3) = f(3)$ to calculate the coefficients $a_j$. This is quick and simple and it will generate the correct values of the $a_j$ if $f(n)$ is indeed a polynomial.
But it won't provide any justification that $f(n)$ really is a polynomial of degree $d + 1$ i.e. that $f(n) = g(n)$ for all non-negative integers $n$. To be more rigorous, we are going to calculate the coefficients a different way...
Let $h(i)$ be the expression in the summation i.e. $h(i) = i^2 \tag{3} $
[Note that you can generalize this method using other polynomial functions for $h$.]
We are going to choose values for the $a_j$ coefficients so that: $$ \begin{align*} g(i) - g(i-1) &= h(i) & \forall i \in \mathbb{N} & \tag{4} \\ \end{align*} $$
Providing we can find such values, this will enable us to prove that $$ \begin{align*} g(n) &= f(n) & \forall n \in \mathbb{N} \end{align*} $$ This is because:
$$ \begin{align*} f(n) &= \sum_{{i}={1}}^{n}h(i) \\ &= \sum_{{i}={1}}^{n}[g(i) - g(i-1)] \\ &= [g(n) - g(n-1)] + [g(n-1) - g(n-2)] + ... + [g(2) - g(1)] + [g(1) - g(0)] \\ &= g(n) - g(0) & \text{because all other terms cancel out} \\ &= g(n) & \text{since } g(0) = 0 \text{ by equation 2} \end{align*} $$
There's some tedious and error-prone algebraic manipulation involved in calculating $g(i) - g(i-1)$. Instead of doing it by hand, let's use symbolic mathematics software to do it for us...
Step 4: Determine the other coefficients programmatically
First let's make some technology choices:
- Use the Python programming language, since it is popular in the Scientific community.
- I already have Python 2.7.10 installed via the PythonXY scientific Python distribution for Windows.
- Use the SymPy Python library as our symbolic Mathematics package.
- Use the iPython notebook as our REPL, as it allows easy sharing of the code.
- Store the notebook in GitHub, which has built-in support for hosting and displaying iPython notebooks.
- Extract the code into a separate Python script, and copy this script into a GitHub gist for easy sharing in the blog.
The first step was to develop the SymPy code in an iPython web notebook. You can download or view the notebook on GitHub.
If you download it, you can then open it from the command line by navigating to a suitable folder and running
ipython notebook --ip=localhost
This will open a local web page which you can use to navigate to the notebook and edit it:
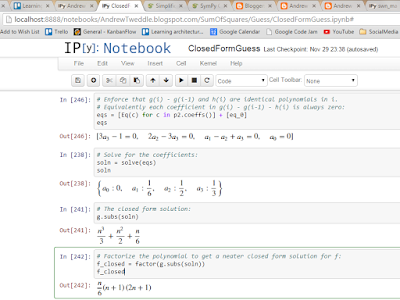
After calculating the coefficients and factorizing the polynomial, the notebook spits out the following formula: $$ \frac{n(n + 1)(2n + 1)}{6} $$
Step 5 (optional): Generalize the code to work for other polynomial summations
After getting the code working using the iPython Notebook, I ported it to a Python script. I then modified the script so that, instead of only supporting the case $h(i) = i^2$, it would accept any polynomial expression in the variable $i$ as a command line parameter.
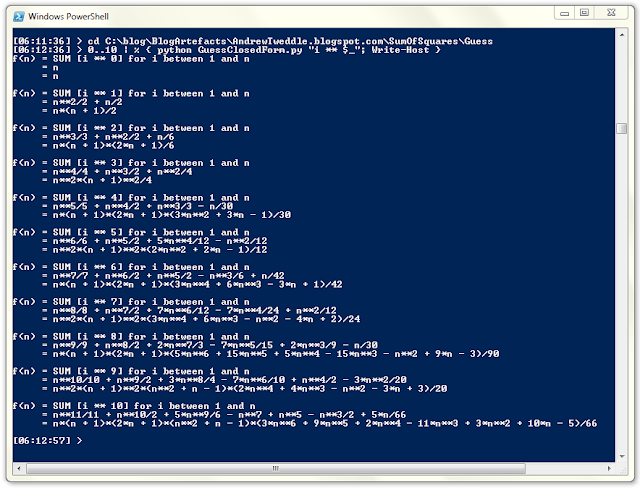
To demonstrate that this method works more generally, I've included a short Powershell snippet to calculate the closed form of the sums of kth powers for k from 0 to 10:
Running this Powershell snippet, produces the following output:
I'm fairly happy with how the Python script turned out in the end. But I found it quite frustrating getting to that point. While SymPy is reasonably well documented at the level of modules and functions, it's harder to work out what the allowed values are for many of the function parameters and what they mean. Although the code is working, there are still quite a few hacks and TODO's left in the code.
As well as using the official SymPy documentation, I also found this SciPy 2011 Tutorial quite useful.
It would have been quicker to do the algebra by hand, although admittedly not for the more general case. Arguably that's also due to my lack of regular practice with SymPy, iPython and Python.
Conclusion
In this blog post I've used SymPy to derive the following result: $$ \sum_{{i}={1}}^{n}i^2 = \frac{n(n + 1)(2n + 1)}{6} $$
In my next few blog posts on this problem, I'm going to demonstrate other derivations of the closed form solution. In particular, I'm looking for derivations which provide greater insight into the problem.
No comments:
Post a Comment