Andrew Loves Math(s)

Introduction

The other day I was discussing Mathematical puzzles with my colleagues and one of them mentioned the "Johnny Hates Math" problem. The problem statement can be found on the SPOJ web site.

Essentially the problem is to insert plus signs at appropriate places in a string of digits such that the resulting sum equals a target value. The plus signs will divide the digits into a set of numbers. None of these numbers should be more than 5 digits long and none should start with a zero, except possibly the number zero itself.

The instructions on the SPOJ web site are to print out the solution with the least number of plus signs. But I think it's more interesting to know the total number of solutions. So I'm just going to provide code to solve that problem, not satisfy the SPOJ specification.

I'm going to solve the problem in a number of different ways and using different programming language features (mainly using Scala). The purpose is to get a feel for which solution methods produce the most concise code and which produce the fastest code. It will also be an opportunity to experiment with Scala and develop more of a feel for the language.

A PowerShell solution

My first attempt was in PowerShell and took 46 minutes to code. A lot of that time was spent fixing PowerShell syntax errors.

Interestingly, I automatically turned to recursion to solve the problem. I guess that's the effect of experimenting with functional programming in the last little while!

My approach was to:

• Branch on the number of digits in the next number (line 6 in the code snippet below)
• Prune each branch based on having enough digits left (line 8), not starting with a zero (line 11), not exceeding the target value (line 16) and not running out of digits before reaching the target value (line 25)
• Recursively call the function with the remaining digits and remaining target value (line 28)
• End the recursion when there are no digits remaining and the target value has been reached exactly (line 21)

A quick comment on line 28: @(...) wraps its contents in an array unless the contents are already an array. This solves a problem in PowerShell where, if a function or script emits multiple values, these values are automatically wrapped in an array - but if there is only a single value, then it is returned as is.

This inconsistency can lead to some very tricky bugs. So it's important to coerce the return value to an array.

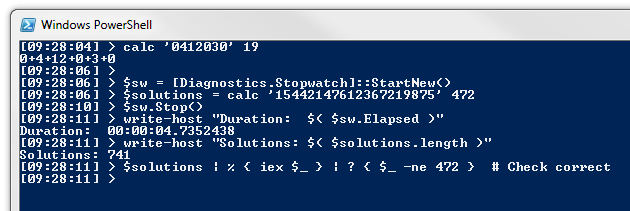
My laptop has an i5-2430M CPU. The PowerShell script solved the problem in under 5 seconds for the problem of inserting plus signs into the left hand side of: 15442147612367219875=472

The break statements provided a very convenient way of excluding infeasible branches. This didn't feel as clean in my first Scala attempt, since Scala treats if statements as expressions (similar to the ?: ternary conditional operator in languages like C# and Java).

---

A few Scala solutions

A Scala base class for the solver algorithm

I refactored the algorithm-independent features into a base class. The code for this is shown below:


I made the somewhat strange decision of defining the abstract solve method to take the same parameters as the class constructor. This was purely to give the derived classes the option of recursively calling the solve method. But it's not a great API design choice. It feels like it is trying to be both a static method (although Scala doesn't have such a concept as it would violate pure OO) and an abstract method.

I'm uncomfortable with this API, which usually means something's wrong. But I'm going to leave it for now, because my focus is on solving the problem, not designing an API.

In line 19, the companion object uses the "SolverUsingFlatMap" derived class as its default solver. I'll provide that sub-class next...

Scala solution 1: SolverUsingFlatMap

The code for my first Scala solution is shown below:


This solver works in a very similar fashion to the PowerShell algorithm. However, instead of returning arrays of strings, it represents a single solution as a List[Int] (i.e. a Scala linked list of integers). A list of solutions is then represented as a List[List[Int]].

I returned an empty list of solutions to indicate that a branch was infeasible. But the break statements in PowerShell felt a bit more intuitive to me.

Scala solution 2: SolverUsingFor

I wanted to get away from returning empty lists as a way of indicating a failed branch. My first thought was to use an Option[List[List[Int]]] type to represent a pruned branch using an option of None. But this felt like overkill.

Instead my second attempt used a for statement to get away from the need to return empty lists. This code turned out to be very concise and pleasing:

Scala solution 3: SolverUsingFoldLeft

I then started wondering whether it was possible to use a foldLeft operation to calculate a solution.

There were a few conceptual issues with making this work. Firstly, a foldLeft is taking a fixed list of items and an initial accumulator, and updating the accumulator for each successive item. In this case, each item was an individual digit.

Secondly, all the previous solutions branched in up to 5 directions at each step. To get branching to work with foldLeft, I needed to store all the branches in the accumulator. To do this, I created a PartialSolution class to keep track of the numbers generated so far, as well as the current number which was being built up. At each step, I would then split each PartialSolution into at most 2 new PartialSolutions, by either terminating the current number or adding another digit to it.

The code is shown below:


This code is considerably more verbose. I also didn't expect it to perform very well. Firstly, it is effectively doing a breadth-first search. Secondly I would expect it to be more memory-intensive and memory access is often much slower than computation. This is partially mitigated by storing the numbers in reverse order (so that large parts of the previous level's data structures are reused, since prepending a number to a list does not create a new list). Also, the foldLeft is tail recursive.

I also expected the foldLeft solution to degrade very quickly for large target totals, as the number of partial solutions is potentially doubling in size at every step. So with a large target value, the pruning effect of comparing the running total to the target is lost.

It turns out that this solver performed a lot better than I expected. And although it did degrade more with larger totals, the effect was not as pronounced as I had been expecting.

Scala worksheet to compare performance of the solvers

I used a Scala worksheet to test the code and compare performance of the various algorithms. The worksheet code and results are shown below:

[UPDATE: This way of measuring performance is not ideal, as explained in this blog post by Aleksey Shipilёv. Rather use a micro-benchmarking framework, such as JMH (possibly with sbt-jmh) or ScalaMeter.]

I tested the 3 solvers twice - first using a low target value, and then again using a high target value (to get an idea of the scalability of the algorithms).

There are some interesting things to note here.

Firstly, the flatMap method was fastest in all cases.

Despite being so short, the method using for comprehensions was much slower. In fact, for the smaller target value, I was quite surprised to see that the breadth-first foldLeft solver was sometimes faster!

With a much larger value, the foldLeft solver showed its poor scalability. However it wasn't that much worse than the method using the for comprehension.

All the Scala solvers were much faster than the PowerShell algorithm. This isn't too surprising, since PowerShell is an interpreted scripting language.

---

Impressions of Scala

Last year I completed the two Scala courses given on Coursera. This was my first foray into Scala since completing those courses. So what are my impressions of the language?

Programming in the small

Firstly, I've really enjoyed solving this problem with Scala. As with F#, I love being able to have concise, readable code - not unlike a dynamically typed language - and yet still gain the benefits of type safety and good performance.

I can see how functional programming in general provides a great solution for "programming in the small".

Scripting

Scripting is another aspect of programming in the small. So at some point I'd like to experiment with using the Scala REPL for writing scripts.

There is definitely promise in this area. I've had a lot of experience using PowerShell for scripting at work and at home. But I've had colleagues demonstrate that they can generally match the features of PowerShell using the F# REPL. It's obvious that functional programming languages can mount a credible challenge in this space - at least from a language perspective. The major advantage PowerShell continues to have in a work setting is its ubiquity on Windows servers.

I also recently finished working on a "record linkage" challenge in my spare time using Python and Pandas for the data munging. If and when time permits, I would like to re-develop the project in Scala to see which code base is easier to work with.

Programming in the large

Something I really like about Scala is that it is clearly designed for "programming in the large" as well. It's not just about functional programming. The baby has not been thrown out with the bathwater: object orientation is treated as an equal citizen in the language.

Actually I'd argue that Scala's true potential in the enterprise has very little to do with being a functional programming language. There are many Scala features which allow very concise, readable Object-Oriented code to be written. This succinctness is part of the style of functional programming. However the overtly functional features in Scala are often too easily abused and could be a distraction from the very real value that Scala offers.

I've seen a number of recent indicators that Scala may be ready to break into the enterprise development space:

• The January 2014 issue of the Thoughtworks technology radar places "Scala - The good parts" in the adopt category at the centre of the radar.
• Rod Johnson is the creator of the Spring framework. In his keynote address at ScalaDays 2013, he stated his opinion that by 2018 Scala would be the leading "new" language and that it would find its niche as the leading enterprise language.
• Vaughn Vernon, author of "Implementing Domain-Driven Design", has recently been blogging about using Scala and Akka for Domain-Driven Design. Tomorrow I will be attending a 3 day workshop given by Vaughn. So I'm looking forward to hearing his opinions on Scala.
• The frequently down (and out?) HammerPrinciple.com web site provides survey-based comparisons of various programming languages. Scala ranked first (above C# and Java) for "this language is best for very large projects", second for "I would use this language for writing server programs" and third for "this language is good for distributed computing".

On the other hand...

Scala has momentum. But that doesn't mean it will achieve breakthrough. Numerous great languages have fallen by the wayside, and there's no guarantee that Scala won't join their ranks. It's a big leap from a language being ready for the enterprise, to the enterprise being ready for a language!

On the negative side, Scala has a lot of very advanced language features which can easily trip up newcomers. This complexity is a substantial barrier to enterprise adoption.

This explains why Thoughtworks qualifies its recommendation of Scala as being just "the good parts".

Rod Johnson also addresses this issue in the ScalaDays keynote mentioned earlier, emphasizing the need to favour readability over poetry.

Martin Odersky, the designer of the Scala language, is well aware of the challenge. In 2011 he provided a list of language features with recommendations for which features were suitable for different levels of application developers and which for library designers.

Library design

This raises another area where Scala appears to be very elegant... library design.

The hammerprinciple.com site has Scala at number 3 for "I rarely have difficulty abstracting patterns I find in my code" and "this language is expressive". It comes in at number 2 for "I find code written in this language is very elegant". These suggest that Scala could be a great language for designing libraries for Scala and the JVM.

Of course you have to take this with a pinch of salt, since early adopters are likely to bias the HammerPrinciple survey outcomes. However there seems to be enough promise here to justify further experimentation.

On that note, there were some things in my JHM code that I really didn't like. I want to refactor the solve() method. And even though it's only in a worksheet, I'd also like to get rid of the implicit parameter to the time() function. It's one of those features which can easily make a code base more opaque. And even though the way I've used it is fairly transparent, just the act of using it legitimizes its use by less experienced programmers (who either haven't developed the intuition to know when not to use the feature, or don't yet have the ability to hold their peers to account by being able to explain the reasoning behind that intuition).

In a later post I'd like to refactor the code for reusability, and in so doing understand more of Scala's library design features.

---

Conclusion

This has been an interesting algorithmic challenge and I have really enjoyed solving it with Scala.

I've seen enough promise with Scala to justify using it as my preferred hobby language (along with Python for experimenting with Data Analytics and data munging).

It's been a lot of fun programming with Scala. And that's pretty important, because there's no guarantee that it will ever become a marketable skill.

RIP Amber

Today we took our beautiful bull mastiff to be put down. Heart-breaking, but necessary... she was over 10 years old and had been diagnosed with kidney failure. She was skipping meals and her weight had dropped to just 34 kilograms (from 51 kg a few years before).

She had a wonderful sniff around the vet's waiting room, and it was lovely to see some of her old joy and bounciness back. But it also brought back memories of her younger self. It made it all the sadder to say good-bye and stroke her head as she fell asleep for the last time...

RIP, Amber!

Birthday Board Games Bash

Thank you!

Firstly, a big thank you to my wonderful wife for arranging a board games party on Saturday for my birthday.

Around 40 friends attended, with the numbers being fairly evenly split between adults and children. We started at 10:00 am, and things went very smoothly, despite a power outage to replace some stolen electrical cable in the area.

There were 3 separate groups of friends present. I was a little apprehensive as it's always difficult to mix different social groups together. But it went really well.

---

Ricochet Robots

We started out playing Ricochet Robots as it can handle an arbitrary number of people and it's easy to join or leave at any time. It's a very clever competitive puzzle and it can be a real brain-burner. It's not everyone's cup of tea, but I love it!

There are online versions at http://www.ricochetrobot.com and http://www.ricochetrobots.com.

---

The Resistance: Avalon

Two of my friends had brought along copies of Avalon (the Resistance) so we then split into two groups - one for novices and the other for the experts. I played in the expert group, but felt a bit out of my depth at first.

There are a group of us who play games once a week after work. The rest of the guys have been playing Avalon a lot over the past few months and even have their own terminology now. But over that time I was temporarily seconded to another project to produce an architecture document for a client. So I have a lot of catching up to do.

---

A present!

Although everyone had been instructed not to bring presents, my colleagues clubbed together to buy me a present anyway. They had colluded with my wife, who had sneakily found out which games were on my most desired list. So I received a copy of Libertalia.

This game has been a big hit in our weekly after-work games sessions. It's a lot of fun to play. So I was delighted!

---

Ultimate Werewolf

After one of the Avalon owners left the party, we ended up with around 15 people still wanting to play. Although the Resistance improves on Werewolf in just about every way, it only caters for up to 10 players. Werewolf can handle much more than that.

So we switched over to a few games of Ultimate Werewolf instead. Great fun as always!

---

The birthday buffoon!

As numbers dwindled, we switched back to Avalon again. We ended with an absolutely excellent game, where the minions of Mordred won all 3 quests and also knew who Merlin was.

I ended up being a perfect patsy for two of the minions of Mordred, who inveigled their way into the trusted group. It was so impressive to see how cleverly they pulled the wool over our eyes, that I felt honoured to have been part of the game - even if I was one of the ones who had been so comprehensively fooled by them.

Usually our monthly board games events last until late into a Saturday night, but this time everyone was gone before supper.

---

And thanks again!

All in all, it was a really fun way to spend a birthday. Thanks to everyone who attended, and made this an ideal birthday party for me!

Researching the Josephus problem

---

All posts in this series:

• One Potato: A description of the problem
• Two potato: The basic equations
• Three potato: An algebraic formula for the last person left
• Four: A neat calculation method using binary numbers
• Five potato: F# functions to check the various formulae
• Six potato: Using a calculation graph to see the pattern
• Seven potato: Generalizing to other intervals
• More: An efficient algorithm for arbitrary intervals
• Online research: In which I discover that it is called the Josephus problem

---

Introduction

This is the ninth post in a series about an interesting Mathematical problem known as the Josephus problem.

Imagine a number of people sitting in a circle. Every second person is asked to leave the circle. This continues until only one person is left. If you label the people 1 to n, what is the label of this last person?

In the first 6 posts in the series:

• I derived a formula for the label of the last person left,
• I provided various proofs of the formula, and
• I wrote code in the F# programming language to calculate the answer in various ways.

In the seventh and eighth posts I created an efficient algorithm for calculating the answer when the number of people skipped is not two but some arbitrary interval k. But I wasn't able to find a closed formula. And I felt I had gone as far as I could on my own. It was time to see how other people had solved the problem.

This post is about what I discovered.

---

The problem has a name

The first thing I discovered is that the problem has a name. It is known as the Josephus problem and it is widely used in Mathematical and Programming challenges. So I will be updating the previous posts to reflect the accepted name.

You can read more about the history of the Josephus problem on Wikipedia or Wolfram Mathworld.

---

In search of an elegant solution

My own attempt

When there are n people in the circle labelled 1 to n, the formula for the last person left in the circle is: $$ f(n) = 2n + 1 - 2^{{\lfloor log_2 n \rfloor} + 1} \tag{1} $$
In the third post in the series I used algebra to prove this result. But although algebra is a very powerful tool for proving the formula, it doesn't give any insight into why the formula is true.

One of the challenges I set myself was to provide that insight. The closest I came was in the sixth post in the series, where I used a calculation graph to show the pattern of values for $f(n)$.

Chamberlain's solution is much more elegant...

Chamberlain's solution

Chamberlain's Solution can be found on page 403 of Problem Solving and Recreational Mathematics 2012 by Paul Yiu of Florida Atlantic University.

His solution is based on a few key insights. I've paraphrased these as follows:

1. When the number of people in the circle is a power of two, the last person left is the first person skipped. This is because:
   
   1. All the even numbered people are skipped each time around the circle
   2. Exactly half the people are eliminated, so the remaining size of the circle is again a power of two
   3. Person one will still be the first person skipped on the next traversal of the circle
   4. So the process repeats itself with the circle halving each time, until person one is the only person left


2. Suppose the size of the circle is $2^m + r$ (with $0 \le r < 2^m$). Carry out the first $r$ removals. Then:
   
   1. The first $r$ people removed are persons $2, 4, 6, ..., 2r$
   2. The next person to be skipped will be person $2r + 1$
   3. This leaves a new, smaller circle with $2^m$ people
   4. So we can apply the rule from point 1 above (for a circle of size $2^m$)
   5. So person $2r + 1$ will be the last person left in the circle

Making it rigorous

There are a few points above which may not be obvious. Let's try to make them more rigorous:

In point 2.a., the assumption is made that the labels of the first $r$ people removed would not "clock over" (i.e. one revolution of the circle hasn't been completed). Is this assumption reasonable?

$$ \begin{align*} \text {By definition: } 0 & \le r < 2^m \tag{2} \\ \text {and: } n & = 2^m + r \tag{3} \\ \\ \therefore 2r & < 2^m + r &\text{ by adding r to both sides of the inequality on the right of (2)}\\ \text{i.e. } 2r & < n \tag{4} \\ \\ \text{Also: } 2r + 1 & \le n \tag{5} \end{align*} $$
Equation 4 shows that this is a reasonable assumption.

In point 2.b. we also assumed that the next person to be skipped will be person $2r + 1$. Equation 5 proves that this label doesn't "clock over" either.

So this proves that $f(2^m + r) = 2r + 1 \text{ where } 0 \le r < 2^m$.

And this can be re-expressed in terms of logarithm and floor functions by noting that:
$$ \begin{align*} 0 & \le r < 2^m & \text{ from equation 2} \\ \therefore 2^m & \le 2^m + r < 2^m + 2^m \\ \therefore 2^m & \le n < 2^{m+1} & \text{ from equation 3} \\ \therefore m & \le \log_2{n} < m+1 & \text{ since logarithms are monotonic (order-preserving) } \\ \therefore m & = {\lfloor log_2 n \rfloor} \tag{6} \\ \\ \text{So:} \\ f(n) & = 2r + 1 \\ & = 2( n - 2^m ) + 1 & \text{ from equation 3}\\ & = 2n + 1 - 2^{m+1} \\ & = 2n + 1 - 2^{{\lfloor log_2 n \rfloor} + 1} & \text{ from equation 6} \end{align*} $$
And this is the formula given in equation 1 earlier.

A beautiful visualization of Chamberlain's solution

You can find a beautiful visual explanation of this solution on the Exploring Binary web site.

Another very succinct solution

I was also very impressed by this solution. But although it was very succinct, I didn't feel that it provided the same "aha" moment of Chamberlain's solution.

---

Generalizing the Josephus problem to arbitrary intervals

I found two algorithms for generalizing the Josephus problem to arbitrary intervals.

Jakobczyk's algorithm

One of these was in a paper entitled On the Generalized Josephus Problem by F Jakobczyk. Although interesting in its own right, I'm rather going to concentrate on the other algorithm I found, as it was far more elegant...

The Ahrens-Schubert algorithm

I found the first page of an article by I. M. Davids published by the Applied Probability Trust. This page gives a very elegant algorithm for the Josephus problem generalized to arbitrary intervals. But since only the first page (with the abstract) is provided, I don't have a proof for the algorithm.

The Ahrens-Schubert solution uses a number series known as an Ahrens array. These are also referred to in the paper as "rounded up" arrays. They are similar to geometric sequences, except that the answer is rounded up after every step. So each term is the previous term multiplied by a factor $f$ and then rounded up to the nearest integer.

Suppose $a_0$ is the initial integer term. Then: $$ \begin{align*} a_1 & = \lceil{a_0 . f}\rceil & \\ a_2 & = \lceil{a_1 . f}\rceil & = \lceil{\lceil{a_0 . f} \rceil . f} \rceil \\ & ... \\ a_m & = \lceil{a_{m-1} . f}\rceil &= \overbrace{\lceil{ \text{ ... } \lceil{\lceil{a_0 . f} \rceil . f} \rceil} \text{ ... } .f \rceil}^\text{m times} \\ \end{align*} $$

The Ahrens-Schubert solution works by finding the largest number (say $a_{m}$) in this series which is less than $kn+1$, where $k$ is the interval to skip and $n$ is the number of people in the circle. The answer is then $ kn + 1 - a_m$.

But what are the values for $a_0$ and $f$ in the rounded up series?

Well, one neat thing about the Ahrens-Schubert solution, is that by choosing different values for $a_0$ it can determine not just the last person left in the circle, but any arbitrary $e^\text{th}$ person removed from the circle. Here are the parameters: $$ \begin{align*} f & = \frac{k}{k-1} \\ a_0 & = k(n - e) + 1 \\ \therefore a_0 & = 1 & \text{when determining the last person left in the circle (set } e = n \text{)}\\ \end{align*} $$

The Ahrens-Schubert solution for $k = 2$

Something else I like about the Ahrens-Schubert solution is how cleanly the closed formula for $k = 2$ emerges from the algorithm. When $k = 2$: $$ \begin{align*} f & = \frac{2}{2 - 1} = 2 \\ a_0 & = k(n - e) + 1 = 2(n-e) + 1 \\ \text{ or: } a_0 & = 1 & \text{for the last person left in the circle}\\ \therefore a_m & = \overbrace{\lceil{ \text{ ... } \lceil{\lceil{a_0 . f} \rceil . f} \rceil} \text{ ... } .f \rceil}^\text{m times} \\ & = \overbrace{\lceil{ \text{ ... } \lceil{\lceil{1 . 2} \rceil . 2} \rceil} \text{ ... } .2 \rceil}^\text{m times} \\ & = 2^m &\text{since the ceiling falls away as all terms are integers} \end{align*} $$ So the answer is $2n + 1 - 2^m$ where $2^m$ is the largest value of $a_i = 2^i$ less than $2n + 1$. And this reduces to equation 1!

My implementation of the Ahrens-Schubert algorithm

Below is my implementation of the algorithm in F#:

let rec getLargestTermInRoundedUpGeometricSeriesBelow 
        (startValue:int) (factor:double) boundary =
    if startValue >= boundary then
        raise (
            System.ArgumentException(
                "The starting element in the series is not below the bound!"))
    else
        let nextValue = int (System.Math.Ceiling( (double startValue) * factor ))
        if nextValue >= boundary then
            startValue
        else
            getLargestTermInRoundedUpGeometricSeriesBelow nextValue factor boundary

let calcEliminationNumberInCircleWithIntervalByRoundedUpSeries 
        eliminationIndex interval sizeOfCircle =
    let dInterval = double interval
    let factor = dInterval / (dInterval - 1.0)
    let bound = interval * sizeOfCircle + 1
    let initialValue = interval * (sizeOfCircle - eliminationIndex) + 1
    bound - getLargestTermInRoundedUpGeometricSeriesBelow initialValue factor bound

let calcLastLeftInCircleWithIntervalByRoundedUpSeries interval sizeOfCircle =
    calcEliminationNumberInCircleWithIntervalByRoundedUpSeries sizeOfCircle interval sizeOfCircle

Performance of the Ahrens-Schubert algorithm

Below are timings for the algorithm:

These are the same inputs as I used in my own algorithm from post 8 of the series, shown below:

Comparing the timings, you can see that the Ahrens-Schubert algorithm is noticeably faster. It took 0.9 seconds to my algorithm's 1.2 seconds when k = 2, and 2.4 seconds versus 2.6 seconds when k = 100.

---

Other references

Code to solve the Josephus problem

Implementations in a variety of languages can be found on the Rosetta Code web site.

More research on the Josephus problem

I found an extensive list of references to the Josephus problem on the puzzlemuseum.com web site. Professor David Singmaster has provided a list of articles on recreational Mathematics. Page 4 of source document 3 lists a large number of articles on the Josephus problem.

---

Conclusion

In this series of articles, I have tackled and successfully solved the Josephus problem. This includes finding an efficient algorithm when the problem is generalized so that an arbitrary number of people is skipped.

I have discovered that this is a well-known problem with an extensive history and a number of explanations and algorithms, including two that were extremely elegant. This makes it an ideal problem to tackle yourself, as there are extensive online resources to compare your approach against.

Using F# to implement various algorithms has been particularly rewarding. This has piqued my interested in functional programming. As a result, I have started dabbling in Haskell. I also recently completed Martin Odersky's Functional Programming Principles in Scala course on Coursera and the follow-up course on the Principles of Reactive Programming. These are thoroughly enjoyable courses, which I recommend highly.

But I'm glad to be finally wrapping up this series on the Josephus problem. It's definitely time to move onto something new!

---