Sunday, March 02, 2014

Andrew Loves Math(s)

Introduction

The other day I was discussing Mathematical puzzles with my colleagues and one of them mentioned the "Johnny Hates Math" problem. The problem statement can be found on the SPOJ web site.

Essentially the problem is to insert plus signs at appropriate places in a string of digits such that the resulting sum equals a target value. The plus signs will divide the digits into a set of numbers. None of these numbers should be more than 5 digits long and none should start with a zero, except possibly the number zero itself.

The instructions on the SPOJ web site are to print out the solution with the least number of plus signs. But I think it's more interesting to know the total number of solutions. So I'm just going to provide code to solve that problem, not satisfy the SPOJ specification.

I'm going to solve the problem in a number of different ways and using different programming language features (mainly using Scala). The purpose is to get a feel for which solution methods produce the most concise code and which produce the fastest code. It will also be an opportunity to experiment with Scala and develop more of a feel for the language.

A PowerShell solution

My first attempt was in PowerShell and took 46 minutes to code. A lot of that time was spent fixing PowerShell syntax errors.

Interestingly, I automatically turned to recursion to solve the problem. I guess that's the effect of experimenting with functional programming in the last little while!

My approach was to:
  • Branch on the number of digits in the next number (line 6 in the code snippet below)
  • Prune each branch based on having enough digits left (line 8), not starting with a zero (line 11), not exceeding the target value (line 16) and not running out of digits before reaching the target value (line 25)
  • Recursively call the function with the remaining digits and remaining target value (line 28)
  • End the recursion when there are no digits remaining and the target value has been reached exactly (line 21)

A quick comment on line 28: @(...) wraps its contents in an array unless the contents are already an array. This solves a problem in PowerShell where, if a function or script emits multiple values, these values are automatically wrapped in an array - but if there is only a single value, then it is returned as is.

This inconsistency can lead to some very tricky bugs. So it's important to coerce the return value to an array.

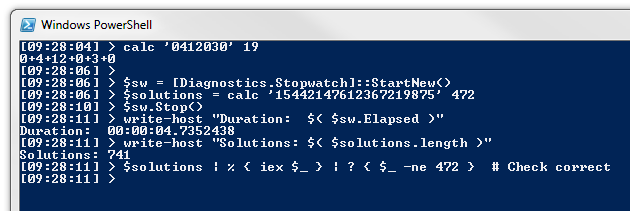
My laptop has an i5-2430M CPU. The PowerShell script solved the problem in under 5 seconds for the problem of inserting plus signs into the left hand side of: 15442147612367219875=472


The break statements provided a very convenient way of excluding infeasible branches. This didn't feel as clean in my first Scala attempt, since Scala treats if statements as expressions (similar to the ?: ternary conditional operator in languages like C# and Java).

A few Scala solutions


A Scala base class for the solver algorithm

I refactored the algorithm-independent features into a base class. The code for this is shown below:


I made the somewhat strange decision of defining the abstract solve method to take the same parameters as the class constructor. This was purely to give the derived classes the option of recursively calling the solve method. But it's not a great API design choice. It feels like it is trying to be both a static method (although Scala doesn't have such a concept as it would violate pure OO) and an abstract method.

I'm uncomfortable with this API, which usually means something's wrong. But I'm going to leave it for now, because my focus is on solving the problem, not designing an API.

In line 19, the companion object uses the "SolverUsingFlatMap" derived class as its default solver. I'll provide that sub-class next...

Scala solution 1: SolverUsingFlatMap

The code for my first Scala solution is shown below:


This solver works in a very similar fashion to the PowerShell algorithm. However, instead of returning arrays of strings, it represents a single solution as a List[Int] (i.e. a Scala linked list of integers). A list of solutions is then represented as a List[List[Int]].

I returned an empty list of solutions to indicate that a branch was infeasible. But the break statements in PowerShell felt a bit more intuitive to me.

Scala solution 2: SolverUsingFor

I wanted to get away from returning empty lists as a way of indicating a failed branch. My first thought was to use an Option[List[List[Int]]] type to represent a pruned branch using an option of None. But this felt like overkill.

Instead my second attempt used a for statement to get away from the need to return empty lists. This code turned out to be very concise and pleasing:


Scala solution 3: SolverUsingFoldLeft

I then started wondering whether it was possible to use a foldLeft operation to calculate a solution.

There were a few conceptual issues with making this work. Firstly, a foldLeft is taking a fixed list of items and an initial accumulator, and updating the accumulator for each successive item. In this case, each item was an individual digit.

Secondly, all the previous solutions branched in up to 5 directions at each step. To get branching to work with foldLeft, I needed to store all the branches in the accumulator. To do this, I created a PartialSolution class to keep track of the numbers generated so far, as well as the current number which was being built up. At each step, I would then split each PartialSolution into at most 2 new PartialSolutions, by either terminating the current number or adding another digit to it.

The code is shown below:


This code is considerably more verbose. I also didn't expect it to perform very well. Firstly, it is effectively doing a breadth-first search. Secondly I would expect it to be more memory-intensive and memory access is often much slower than computation. This is partially mitigated by storing the numbers in reverse order (so that large parts of the previous level's data structures are reused, since prepending a number to a list does not create a new list). Also, the foldLeft is tail recursive.

I also expected the foldLeft solution to degrade very quickly for large target totals, as the number of partial solutions is potentially doubling in size at every step. So with a large target value, the pruning effect of comparing the running total to the target is lost.

It turns out that this solver performed a lot better than I expected. And although it did degrade more with larger totals, the effect was not as pronounced as I had been expecting.

Scala worksheet to compare performance of the solvers

I used a Scala worksheet to test the code and compare performance of the various algorithms. The worksheet code and results are shown below:

[UPDATE: This way of measuring performance is not ideal, as explained in this blog post by Aleksey Shipilёv. Rather use a micro-benchmarking framework, such as JMH (possibly with sbt-jmh) or ScalaMeter.]

I tested the 3 solvers twice - first using a low target value, and then again using a high target value (to get an idea of the scalability of the algorithms).

There are some interesting things to note here.

Firstly, the flatMap method was fastest in all cases.

Despite being so short, the method using for comprehensions was much slower. In fact, for the smaller target value, I was quite surprised to see that the breadth-first foldLeft solver was sometimes faster!

With a much larger value, the foldLeft solver showed its poor scalability. However it wasn't that much worse than the method using the for comprehension.

All the Scala solvers were much faster than the PowerShell algorithm. This isn't too surprising, since PowerShell is an interpreted scripting language.

Impressions of Scala

Last year I completed the two Scala courses given on Coursera. This was my first foray into Scala since completing those courses. So what are my impressions of the language?

Programming in the small

Firstly, I've really enjoyed solving this problem with Scala. As with F#, I love being able to have concise, readable code - not unlike a dynamically typed language - and yet still gain the benefits of type safety and good performance.

I can see how functional programming in general provides a great solution for "programming in the small".

Scripting

Scripting is another aspect of programming in the small. So at some point I'd like to experiment with using the Scala REPL for writing scripts.

There is definitely promise in this area. I've had a lot of experience using PowerShell for scripting at work and at home. But I've had colleagues demonstrate that they can generally match the features of PowerShell using the F# REPL. It's obvious that functional programming languages can mount a credible challenge in this space - at least from a language perspective. The major advantage PowerShell continues to have in a work setting is its ubiquity on Windows servers.

I also recently finished working on a "record linkage" challenge in my spare time using Python and Pandas for the data munging. If and when time permits, I would like to re-develop the project in Scala to see which code base is easier to work with.

Programming in the large

Something I really like about Scala is that it is clearly designed for "programming in the large" as well. It's not just about functional programming. The baby has not been thrown out with the bathwater: object orientation is treated as an equal citizen in the language.

Actually I'd argue that Scala's true potential in the enterprise has very little to do with being a functional programming language. There are many Scala features which allow very concise, readable Object-Oriented code to be written. This succinctness is part of the style of functional programming. However the overtly functional features in Scala are often too easily abused and could be a distraction from the very real value that Scala offers.

I've seen a number of recent indicators that Scala may be ready to break into the enterprise development space:

On the other hand...

Scala has momentum. But that doesn't mean it will achieve breakthrough. Numerous great languages have fallen by the wayside, and there's no guarantee that Scala won't join their ranks. It's a big leap from a language being ready for the enterprise, to the enterprise being ready for a language!

On the negative side, Scala has a lot of very advanced language features which can easily trip up newcomers. This complexity is a substantial barrier to enterprise adoption.

This explains why Thoughtworks qualifies its recommendation of Scala as being just "the good parts".

Rod Johnson also addresses this issue in the ScalaDays keynote mentioned earlier, emphasizing the need to favour readability over poetry.

Martin Odersky, the designer of the Scala language, is well aware of the challenge. In 2011 he provided a list of language features with recommendations for which features were suitable for different levels of application developers and which for library designers.

Library design

This raises another area where Scala appears to be very elegant... library design.

The hammerprinciple.com site has Scala at number 3 for "I rarely have difficulty abstracting patterns I find in my code" and "this language is expressive". It comes in at number 2 for "I find code written in this language is very elegant". These suggest that Scala could be a great language for designing libraries for Scala and the JVM.

Of course you have to take this with a pinch of salt, since early adopters are likely to bias the HammerPrinciple survey outcomes. However there seems to be enough promise here to justify further experimentation.

On that note, there were some things in my JHM code that I really didn't like. I want to refactor the solve() method. And even though it's only in a worksheet, I'd also like to get rid of the implicit parameter to the time() function. It's one of those features which can easily make a code base more opaque. And even though the way I've used it is fairly transparent, just the act of using it legitimizes its use by less experienced programmers (who either haven't developed the intuition to know when not to use the feature, or don't yet have the ability to hold their peers to account by being able to explain the reasoning behind that intuition).

In a later post I'd like to refactor the code for reusability, and in so doing understand more of Scala's library design features.

Conclusion

This has been an interesting algorithmic challenge and I have really enjoyed solving it with Scala.

I've seen enough promise with Scala to justify using it as my preferred hobby language (along with Python for experimenting with Data Analytics and data munging).

It's been a lot of fun programming with Scala. And that's pretty important, because there's no guarantee that it will ever become a marketable skill.
Posted by at
Labels: , , , , ,

No comments:

Post a Comment

Subscribe to: Post Comments (Atom)